Managing attributes (tutorial)
This trail introduces you to the full power of visone's attribute manager and shows you how to select elements dependent on attribute values. The attribute manager allows you, for instance, to convert tie strength to distance or rankings and vice versa, dichotomize networks, rescale tie weights and much more.
An exemplary dataset: Newcomb Fraternity Data
The Newcomb Fraternity Data (see Newcomb T. (1961). The acquaintance process. New York: Holt, Reinhard & Winston.) consits of 15 matrices recording weekly sociometric preference rankings from 17 men attending the University of Michigan in the fall of 1956. Each participant ranks all 16 others from best friend down to least friend. This data set is explained in more detail on the page Newcomb Fraternity (data).
To follow the steps illustrated in this trail, you should download the file Newfrat.zip (ZIP file containing the 15 matrices newfrat01.csv to newfrat15.csv), save it to your computer and decompress (unzip) it.
Import the CSV files
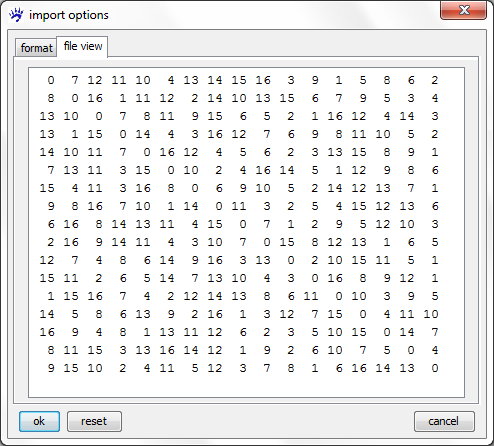
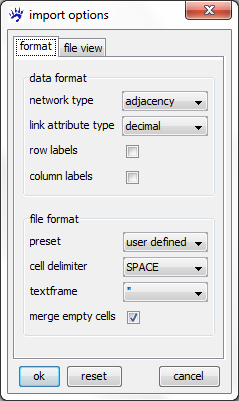
We start by importing one of the adjacency matrices (e.g., newfrat01.csv) into visone. Therefore use the menu file, open and select the file type .csv, .txt. Before importing the file it is important to set the correct options; the images below show the file view tab and the format tab of the import options dialog.
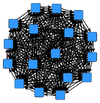
Setting the options as shown in the format tab and clicking on ok opens the network which looks like the one shown on the right.
It can be seen that the network is complete (i.e., each pair of actors is connected by a bidirectional tie. All links have an attribute called csv value whose value corresponds to the respective entry in the adjacency matrix and, thus, is equal to the rank of the target node in the ordered list of friends of the source node.