Simmelian backbone extraction: Difference between revisions
(Created page with "'''Note: this page documents a visone functionality that will be available in the next release of visone (version 2.7, scheduled for May 2013) .''' This network transformation i...") |
No edit summary |
||
| Line 1: | Line 1: | ||
'''Note: this page documents a visone functionality that will be available in the next release of visone (version 2.7, scheduled for May 2013) .''' | '''Note: this page documents a visone functionality that will be available in the next release of visone (version 2.7, scheduled for May 2013) .''' | ||
This | This transformation algorithm is meant to make a network more easy to visualize and analyze, e.g., with regard to detecting an underlying community structure. | ||
It is based on local ranking and overlap calculations to extract a Simmelian backbone of strong and redundant ties. | It is based on local ranking and overlap calculations to extract a ''Simmelian backbone'' of strong and redundant ties. | ||
Detailed information is provided in | Detailed information is provided in | ||
| Line 8: | Line 8: | ||
Background information will also be presented in a talk at XXXIII Sunbelt Social Networks Conference of the International Network for Social Network Analysis (INSNA), | Background information will also be presented in a talk at XXXIII Sunbelt Social Networks Conference of the International Network for Social Network Analysis (INSNA), | ||
Hamburg, Germany, May 21-26, 2013 | Hamburg, Germany, May 21-26, 2013; Bobo Nick, Conrad Lee, Pádraig Cunningham, Ulrik Brandes: "Triadic Cohesion in Social Networks". | ||
| Line 26: | Line 26: | ||
The Simmelian backbone is extracted from a ranked neighborhood graph. | The Simmelian backbone is extracted from a ranked neighborhood graph. | ||
For this purpose, each undirected edge is split into two contrary directed edges, | For this purpose, each undirected edge is split into two contrary directed edges, | ||
and the algorithm will rank each node's (outgoing) neighbors according to an associated (ordinal) '''link strength''' attribute | and the algorithm will rank each node's (outgoing) neighbors according to an associated (ordinal) '''link strength''' attribute: | ||
* If ''uniform'' is selected (default), the algorithm will calculate a link strength attribute on its own (the ''Simmelian strength''; saved as ''triadType300''). | * If ''uniform'' is selected (default), the algorithm will calculate a link strength attribute on its own (the ''Simmelian strength''; saved as ''triadType300''). | ||
* ''Otherwise'', the algorithm will use the attribute that was provided. | * ''Otherwise'', the algorithm will use the attribute that was provided. | ||
Neighbors with equal link strength are equally ranked with the best available rank. | |||
The resulting neighborhood rankings are saved in a link attribute termed ''ranking'' | The resulting neighborhood rankings are saved in a link attribute termed ''ranking''. | ||
(For technical reasons, if the selected link strength attribute is termed ''ranking'' or ''redundancy'' it will be renamed into ''backbone-weight (ranking)'' or ''backbone-weight (redundancy)'', respectively.) | (For technical reasons, if the selected link strength attribute is termed ''ranking'' or ''redundancy'' it will be renamed into ''backbone-weight (ranking)'' or ''backbone-weight (redundancy)'', respectively.) | ||
| Line 39: | Line 39: | ||
Next, for designated pairs of nodes, the algorithm will calculate the redundancy of top-ranked neighbors. | Next, for designated pairs of nodes, the algorithm will calculate the redundancy of top-ranked neighbors. | ||
Always | Always, each redundancy assessment is associated with a directed link (from ego to alter) in the ranked neighborhood graph. | ||
The resulting redundancy values are saved in a link attribute termed ''redundancy''. | The resulting redundancy values are saved in a link attribute termed ''redundancy''. | ||
==== Parametric variant ==== | ==== Parametric variant ==== | ||
If ''parametric'' is selected, the required redundancy for a link to be included in the Simmelian backbone | If '''parametric''' is selected (default), the required redundancy for a link to be included in the Simmelian backbone | ||
is specified in terms of a necessary number of top-ranked common neighbors (regarding ego and alter associated with this link): | is specified in terms of a necessary number of top-ranked common neighbors (regarding ego and alter associated with this link): | ||
* You can use the '''max ranking''' parameter to specify the maximal rank which is still regarded as a top-rank. That is, those outgoing neighbors that have been attached a rank greater than ''max ranking'' will not contribute in the redundancy calculation | * You can use the '''min overlap''' parameter to specify a minimal required overlap of top-ranked common neighbors (default 5). | ||
* You can use the '''max ranking''' parameter to specify the maximal rank which is still regarded as a top-rank (default 10). That is, those outgoing neighbors that have been attached a rank greater than ''max ranking'' will not contribute in the redundancy calculation. | |||
* You can use the '''conditioned''' parameter to specify for which pairs of actors the overlap is calculated: | * You can use the '''conditioned''' parameter to specify for which pairs of actors the overlap is calculated: | ||
** if selected (default), the overlap calculation is only performed for those links which have been top-ranked themselves | ** if selected (default), the overlap calculation is only performed for those links which have been top-ranked themselves | ||
** if deselected, the overlap calculation is performed for each directed link in the ranked neighborhood graph. | ** if deselected, the overlap calculation is performed for each directed link in the ranked neighborhood graph. | ||
''Special cases'' | ''Special cases'': | ||
If ''conditioned'' is true, non-top-ranked links will have undefined overlap values. | |||
If '' | Setting ''min overlap'' to zero will imply that only links with undefined overlap value are removed from the network. | ||
Setting ''min overlap'' to zero will imply that only links with undefined overlap value are removed from the network | |||
==== Non-parametric variant ==== | ==== Non-parametric variant ==== | ||
In the non-parametric variant of the transformation algorithm, a redundancy calculation is triggered for each link in the ranked neighborhood graph. | In the non-parametric variant of the transformation algorithm, a redundancy calculation is triggered for each link in the ranked neighborhood graph. | ||
The redundancy is defined as the maximum Jaccard coefficient that is | The redundancy is defined as the maximum (ranked) Jaccard coefficient that is found when iteratively comparing top ranked neighbors (including more and more ranks). | ||
For a link to be included in the Simmelian backbone, the best found Jaccard coefficient has to be at least one half. | For a link to be included in the Simmelian backbone, the best found Jaccard coefficient has to be at least one half. | ||
==== | ==== Reciprocity handling ==== | ||
For any of the two variants (parametric, or non-parametric redundancy assessment), you can decide whether ego is identified with alter in the redundancy calculations, | For any of the two variants (parametric, or non-parametric redundancy assessment), you can decide whether ego is '''identified''' with alter in the redundancy calculations, | ||
i.e. reciprocity within top ranks is counted as overlap, or whether | i.e. reciprocity within top ranks is counted as overlap (default), or whether ego's rank in alter's neighborhood and alter's rank in ego's neighborhood are not taken into account | ||
in the redundancy assessment. | |||
== Result == | == Result == | ||
Revision as of 10:23, 19 April 2013
Note: this page documents a visone functionality that will be available in the next release of visone (version 2.7, scheduled for May 2013) .
This transformation algorithm is meant to make a network more easy to visualize and analyze, e.g., with regard to detecting an underlying community structure. It is based on local ranking and overlap calculations to extract a Simmelian backbone of strong and redundant ties. Detailed information is provided in
- Bobo Nick, Conrad Lee, Ulrik Brandes: "Simmelian Backbones: Amplifying Hidden Homophily in Facebook Networks", 2013; submitted.
Background information will also be presented in a talk at XXXIII Sunbelt Social Networks Conference of the International Network for Social Network Analysis (INSNA), Hamburg, Germany, May 21-26, 2013; Bobo Nick, Conrad Lee, Pádraig Cunningham, Ulrik Brandes: "Triadic Cohesion in Social Networks".
Please address questions and comments to Bobo Nick.
Where to find
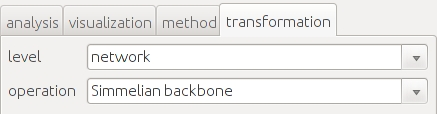
Access is given via the transformation tab in the left-hand side of the visone window: set level to network and operation to Simmelian backbone.
Configuration
Ranking calculation
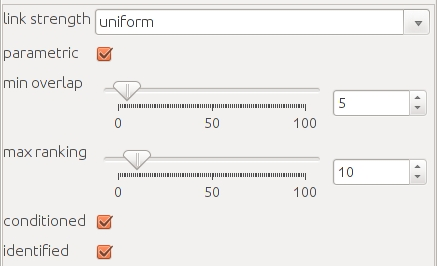
The Simmelian backbone is extracted from a ranked neighborhood graph. For this purpose, each undirected edge is split into two contrary directed edges, and the algorithm will rank each node's (outgoing) neighbors according to an associated (ordinal) link strength attribute:
- If uniform is selected (default), the algorithm will calculate a link strength attribute on its own (the Simmelian strength; saved as triadType300).
- Otherwise, the algorithm will use the attribute that was provided.
Neighbors with equal link strength are equally ranked with the best available rank. The resulting neighborhood rankings are saved in a link attribute termed ranking. (For technical reasons, if the selected link strength attribute is termed ranking or redundancy it will be renamed into backbone-weight (ranking) or backbone-weight (redundancy), respectively.)
Redundancy assessment
Next, for designated pairs of nodes, the algorithm will calculate the redundancy of top-ranked neighbors. Always, each redundancy assessment is associated with a directed link (from ego to alter) in the ranked neighborhood graph. The resulting redundancy values are saved in a link attribute termed redundancy.
Parametric variant
If parametric is selected (default), the required redundancy for a link to be included in the Simmelian backbone is specified in terms of a necessary number of top-ranked common neighbors (regarding ego and alter associated with this link):
- You can use the min overlap parameter to specify a minimal required overlap of top-ranked common neighbors (default 5).
- You can use the max ranking parameter to specify the maximal rank which is still regarded as a top-rank (default 10). That is, those outgoing neighbors that have been attached a rank greater than max ranking will not contribute in the redundancy calculation.
- You can use the conditioned parameter to specify for which pairs of actors the overlap is calculated:
- if selected (default), the overlap calculation is only performed for those links which have been top-ranked themselves
- if deselected, the overlap calculation is performed for each directed link in the ranked neighborhood graph.
Special cases: If conditioned is true, non-top-ranked links will have undefined overlap values. Setting min overlap to zero will imply that only links with undefined overlap value are removed from the network.
Non-parametric variant
In the non-parametric variant of the transformation algorithm, a redundancy calculation is triggered for each link in the ranked neighborhood graph. The redundancy is defined as the maximum (ranked) Jaccard coefficient that is found when iteratively comparing top ranked neighbors (including more and more ranks). For a link to be included in the Simmelian backbone, the best found Jaccard coefficient has to be at least one half.
Reciprocity handling
For any of the two variants (parametric, or non-parametric redundancy assessment), you can decide whether ego is identified with alter in the redundancy calculations, i.e. reciprocity within top ranks is counted as overlap (default), or whether ego's rank in alter's neighborhood and alter's rank in ego's neighborhood are not taken into account in the redundancy assessment.
Result
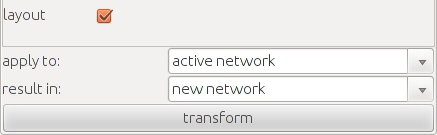
For convenience, if layout is selected, visone's quick layout functionality is used to visualize the modified network structure at the end of the algorithm; otherwise, all node positions remain as before.
Use apply to to select the network(s) for which the calculations shall be performed. Since the network structure is altered by the algorithm, result in a new network rather than this network is proposed as default. The calculation is triggered by clicking the transform button at the bottom.