Closeness: Difference between revisions
No edit summary |
|||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
'''Closeness''' is a radial measure of centrality that favors actors | '''Closeness''' is a radial measure of centrality that favors actors that can reach many others via short paths. Intuitively, if the graph represents a transportation network, then a node with high closeness would make a good location for a warehouse since the average distance to all other locations (i.e., all other nodes in the graph) is relatively short. In information-spreading networks, a node with high closeness centrality would be a good choice to start a rumor since many others can be reached with relatively few intermediates. | ||
== Definition (simple case) == | |||
On directed, unweighted [[graph|graphs]] <math>\displaystyle{G=(V,E)}</math> that are [[Connectivity|strongly connected]], the closeness centrality <math>\displaystyle{c_C(v)}</math> of a node <math>v\in V</math> is defined as the inverse of the sum of distances from <math>v</math> to all other nodes, i.e., it is | |||
<math>c_C(v)=\frac{1}{\sum\limits_{t\in V\setminus v} d_G(v,t)}</math>, | |||
<math> | where <math>\displaystyle{d_G(v,t)}</math> denotes the length of a [[Shortest path|shortest directed path]] from <math>v</math> to <math>t</math>. The definition for [[Connectivity|connected]] undirected graphs is identical with <math>\displaystyle{d_G(v,t)}</math> being defined as the length of a [[Shortest path|shortest path]]. | ||
== Example == | |||
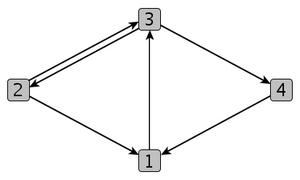
Consider the directed graph below. For example, the length of a shortest path from Node 1 to Node 3 is one while the distance from 3 to 1 equals two, since edges can only be traveled in the specified direction. The length of a shortest path from Node 4 to Node 2 is three; the unique shortest path connecting these nodes is <math>4 \rightarrow 1 \rightarrow 3 \rightarrow 2 </math> | |||
[[File:Closeness_example1.png|300px]] | |||
All pairwise distances are listed in the following matrix where the entry in row <math>u</math> and column <math>v</math> is equal to the distance from node <math>u</math> to node <math>v</math>. | |||
<math> | <math>\begin{bmatrix} | ||
\cdot & 2 & 1 & 2 \\ | |||
1 & \cdot & 1 & 2 \\ | |||
2 & 1 & \cdot & 1 \\ | |||
1 & 3 & 2 & \cdot | |||
\end{bmatrix}</math> | |||
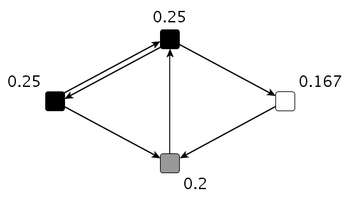
The inverse closeness centrality (i.e., the denominator in the formula above) of node <math>v</math> is equal to the row sum in the above matrix. For instance, the sum of distances from Node 1 to all other nodes is <math>2+1+2=5</math> and, hence, it is <math>\displaystyle{c_C(1)=1/5=0.2}</math>; the sum of distances from Node 4 to all other nodes is <math>1+3+2=6</math> and, hence, it is <math>\displaystyle{c_C(1)=1/6\approx 0.167}</math>. The closeness centrality of all nodes is shown in the image below. | |||
[[File:Closeness_example2.png|350px]] | |||
== Special cases == | == Special cases == | ||
=== Unconnected graphs === | === Unconnected graphs === | ||
The definition of closeness centrality needs to be adapted for cases in which the graph is not strongly connected. Indeed, if a node <math>u</math> is not reachable from another node <math>v</math>, then the distance <math>\displaystyle{d_G(v,u)}</math> is undefined (or sometimes, for convenience, set to <math>\infty</math>, which is no help either) implying that the closeness formula presented above is undefined as well. Furthermore, it would be a bad choice to simply drop the unreachable nodes from the summation, since then adding an outgoing link to a node could actually decrease its closeness centrality in such a way that it looses its closeness rank compared to other nodes. Possibilities to generalize closeness centrality to graphs that are not strongly connected include ... | |||
=== Edge weights and distances === | === Edge weights and distances === | ||
If a [[link length]] has been selected, the length of an <math>(v,t)</math>-path is the sum of the length of all links in the path. | |||
== Implementation in visone == | == Implementation in visone == | ||
| Line 29: | Line 42: | ||
=== Normalization and treatment of special cases === | === Normalization and treatment of special cases === | ||
=== Algorithmic runtime === | '''Standardize''' ... | ||
=== Algorithmic runtime === | |||
The closeness centrality of one node <math>v</math> can be computed by a single [[BFS|breadth-first-search (BFS)]] starting at <math>v</math>. On graphs without edge weights, BFS has a run-time linear in the size of the graph, i.e., in <math>\mathcal{O}(|V|+|E|)</math>. Hence, the closeness of all vertices can be computed in <math>\mathcal{O}(|V|^2+|E|\cdot|V|)</math>. On graphs with varying edge lengths ... | |||
== Related measures == | == Related measures == | ||
* [[Radiality]] | |||
* [[Eccentricity]] | |||
* [[Current-flow closeness]] | |||
== References == | == References == | ||
Latest revision as of 10:35, 11 April 2011
Closeness is a radial measure of centrality that favors actors that can reach many others via short paths. Intuitively, if the graph represents a transportation network, then a node with high closeness would make a good location for a warehouse since the average distance to all other locations (i.e., all other nodes in the graph) is relatively short. In information-spreading networks, a node with high closeness centrality would be a good choice to start a rumor since many others can be reached with relatively few intermediates.
Definition (simple case)
On directed, unweighted graphs that are strongly connected, the closeness centrality of a node is defined as the inverse of the sum of distances from to all other nodes, i.e., it is
,
where denotes the length of a shortest directed path from to . The definition for connected undirected graphs is identical with being defined as the length of a shortest path.
Example
Consider the directed graph below. For example, the length of a shortest path from Node 1 to Node 3 is one while the distance from 3 to 1 equals two, since edges can only be traveled in the specified direction. The length of a shortest path from Node 4 to Node 2 is three; the unique shortest path connecting these nodes is
All pairwise distances are listed in the following matrix where the entry in row and column is equal to the distance from node to node .
The inverse closeness centrality (i.e., the denominator in the formula above) of node is equal to the row sum in the above matrix. For instance, the sum of distances from Node 1 to all other nodes is and, hence, it is ; the sum of distances from Node 4 to all other nodes is and, hence, it is . The closeness centrality of all nodes is shown in the image below.
Special cases
Unconnected graphs
The definition of closeness centrality needs to be adapted for cases in which the graph is not strongly connected. Indeed, if a node is not reachable from another node , then the distance is undefined (or sometimes, for convenience, set to , which is no help either) implying that the closeness formula presented above is undefined as well. Furthermore, it would be a bad choice to simply drop the unreachable nodes from the summation, since then adding an outgoing link to a node could actually decrease its closeness centrality in such a way that it looses its closeness rank compared to other nodes. Possibilities to generalize closeness centrality to graphs that are not strongly connected include ...
Edge weights and distances
If a link length has been selected, the length of an -path is the sum of the length of all links in the path.
Implementation in visone
Normalization and treatment of special cases
Standardize ...
Algorithmic runtime
The closeness centrality of one node can be computed by a single breadth-first-search (BFS) starting at . On graphs without edge weights, BFS has a run-time linear in the size of the graph, i.e., in . Hence, the closeness of all vertices can be computed in . On graphs with varying edge lengths ...