Backbone Layout: Difference between revisions
No edit summary |
(→Method) |
||
| (16 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
=Backbone Layout= | |||
===Method=== | |||
Small-world graphs have characteristically low average distance and thus cause force-directed methods to generate drawings that look like hairballs. | Small-world graphs have characteristically low average distance and thus cause force-directed methods to generate drawings that look like hairballs. | ||
The backbone layout tries to untangle hairball graphs. The method is based on a spanning subgraph that is sparse but connected and consists of strong ties holding together communities. | The backbone layout tries to untangle hairball graphs. The method is based on a spanning subgraph that is sparse but connected and consists of strong ties holding together communities. | ||
Strong ties are identified using a structural measures of embeddedness. | |||
Strong ties are identified using a | |||
More detailed background information is provided in | More detailed background information is provided in | ||
* Arlind Nocaj, Mark Ortmann, and Ulrik Brandes: Untangling Hairballs | * Arlind Nocaj, Mark Ortmann, and Ulrik Brandes: [http://jgaa.info/accepted/2015/NocajOrtmannBrandes2015.19.2.pdf Untangling the Hairballs of Multi-Centered, Small-World Online Social Media Networks], Journal of Graph Algorithms and Applications, 19(2):595-618, 2015. | ||
{| | {| | ||
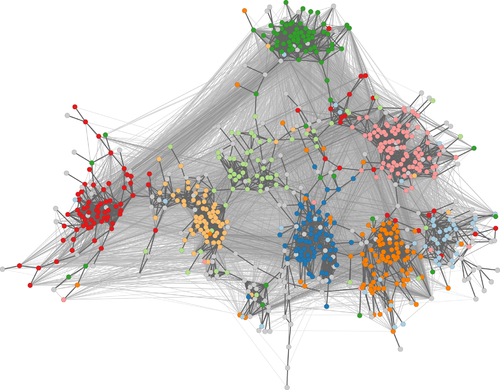
|+ | |+ valign="top"| Facebook friendships at California Institute of Technology (Caltech36). Vertex color corresponds to dormitory (gray for missing values), but has not been utilized in the layout algorithm. The layout in '''(a)''' is based on the entire hairball graph, whereas '''(b)''' uses edge embeddedness which spreads the graph while keeping cohesive groups together. Embeddedness mapped to edge color; backbone edges dark gray. | ||
|- halign="center" | |||
| style="text-align: center;" |[[File:Caltech36-hairball.png|300px]] | |||
|- | |||
| style="text-align: center;" |'''(a)''' drawing based on complete network | |||
|- | |- | ||
| | | style="text-align: center;" |[[File:Caltech36-Quadrilateral-Backbone.png|500px]] | ||
| [[File:Caltech36-Quadrilateral-Backbone.png|500px | |||
|- | |- | ||
| style="text-align: center;" |'''(b)''' drawing based on quadrilateral Simmelian backbone | |||
| style="text-align: center;" |'''(b)''' drawing based on | |||
| | | | ||
|} | |} | ||
=== Complexity === | |||
The computation of the embeddedness together with the backbone extraction scales well for large networks with, e.g., millions of edges and nodes. | |||
The asymptotic runtime is <math> O(|E| \triangle(G))</math> for a graph <math>G=(V,E)</math> where <math>\triangle(G)</math> is the maximum degree of a vertex <math> v\in V</math>. | |||
The final layout based on the extracted backbone needs <math>O(|V|^2)</math> time and memory, which does not scale for very large graphs. | |||
=== Example Data === | |||
A set of 50 synthetic hairball networks with a hidden group structure: | |||
* [[Media:Hairball-Graphs-PPM500.zip|'''Dataset''']] (11 MB) and its [[Hairball_Graphs_(data)| '''Description''']] | |||
Latest revision as of 15:51, 1 February 2016
Backbone Layout
Method
Small-world graphs have characteristically low average distance and thus cause force-directed methods to generate drawings that look like hairballs.
The backbone layout tries to untangle hairball graphs. The method is based on a spanning subgraph that is sparse but connected and consists of strong ties holding together communities. Strong ties are identified using a structural measures of embeddedness.
More detailed background information is provided in
- Arlind Nocaj, Mark Ortmann, and Ulrik Brandes: Untangling the Hairballs of Multi-Centered, Small-World Online Social Media Networks, Journal of Graph Algorithms and Applications, 19(2):595-618, 2015.
Complexity
The computation of the embeddedness together with the backbone extraction scales well for large networks with, e.g., millions of edges and nodes.
The asymptotic runtime is for a graph where is the maximum degree of a vertex .
The final layout based on the extracted backbone needs time and memory, which does not scale for very large graphs.
Example Data
A set of 50 synthetic hairball networks with a hidden group structure:
- Dataset (11 MB) and its Description