Backbone Layout

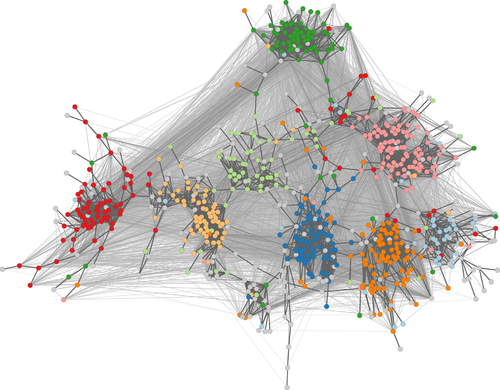
Small-world graphs have characteristically low average distance and thus cause force-directed methods to generate drawings that look like hairballs.

The backbone layout tries to untangle hairball graphs. The method is based on a spanning subgraph that is sparse but connected and consists of strong ties holding together communities.

Strong ties are identified using a measure of embeddedness which is based on a weighted accumulation of triangles in quadrangles.

More detailed background information is provided in

• Arlind Nocaj, Mark Ortmann, and Ulrik Brandes: Untangling Hairballs: From 3 to 14 Degrees of Separation, to appear in Proceedings of the 22nd International Symposium on Graph Drawing (GD 2014).

Facebook friendships at California Institute of Technology (Caltech36). Vertex color corresponds to dormitory (gray for missing values), but has not been utilized in the layout algorithm. The layout in (a) is based on the entire hairball graph, whereas (b) uses edge embeddedness which spreads the graph while keeping cohesive groups together. Embeddedness mapped to edge color; backbone edges dark gray.

(a) drawing based on complete network	(b) drawing based on Quadrilateral backbone

Asymptotic Complexity

The computation of the embeddedness together with the backbone extraction scales well for large networks with, e.g., millions of edges and nodes.

The asymptotic runtime is $O(|E|\triangle (G))$ for a graph $G=(V,E)$ where $\triangle (G)$ is the maximum degree of a vertex $v\in V$.

The final layout based on the extracted backbone needs $O(|V|^{2}$ time and memory, which does not scale for very large graphs.